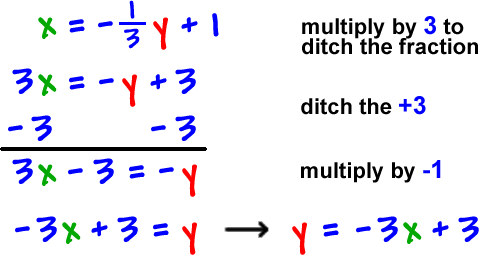
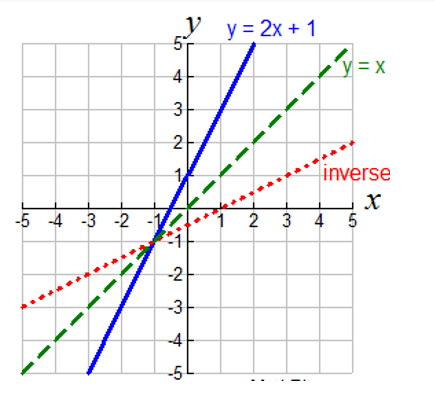
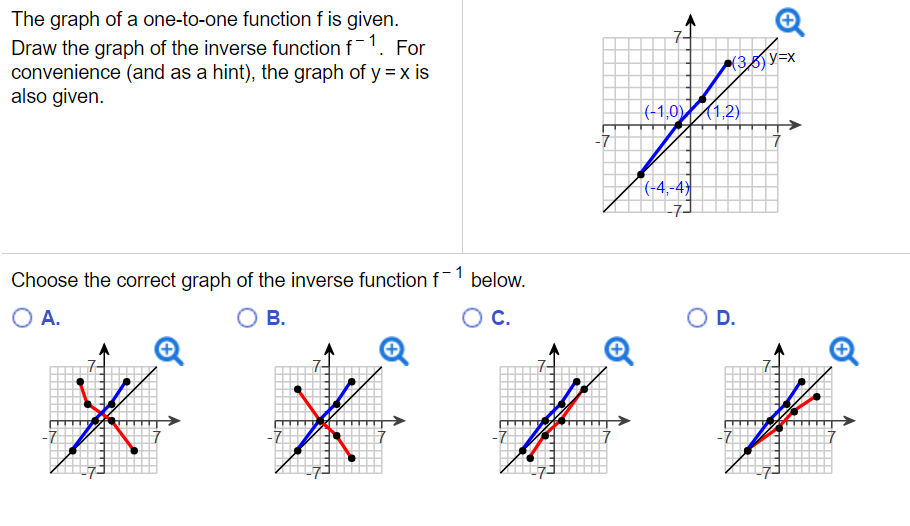
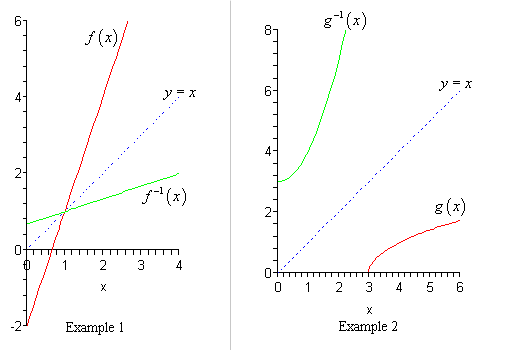
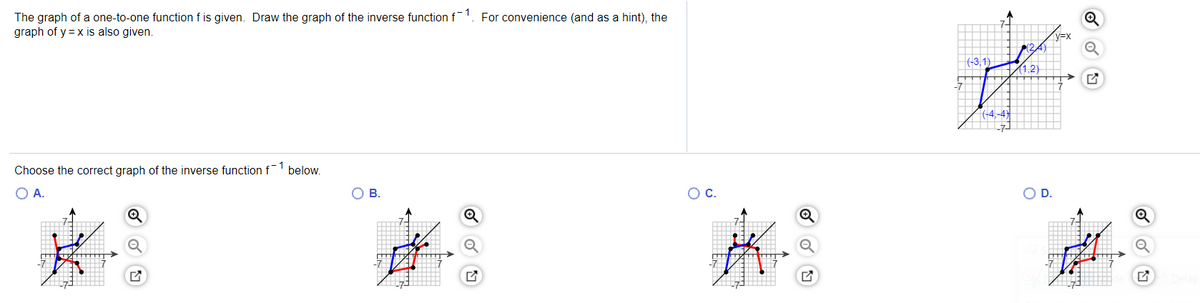
F (x)=3x5 The graph of that function is like this Replace by Interchange x and y Solve for y Replace by Now plot that on the same graph Notice that the inverse is the reflection of the original line in the "identity" line which has equation , called the identity lineThe function f is defined as onetoone (or injective), if each value in domain A corresponds to a different value in range B In other words, no two elements in the domain of the function correspond to the same element in the range It is possible to defineTranscribed image text The graph of a onetoone function f is given Draw the graph of the inverse function f1 For convenience (and as a hint), the graph of y = x is also given 72 (3,1) 11,2) X 74,4) 1 Choose the correct graph of the inverse function f below OA B OD
Use The Graph Of A Function To Graph Its Inverse College Algebra
One to one function inverse graph
One to one function inverse graph-Graphically, we can determine if a function is $11$ by using the Horizontal Line Test, which states A graph represents a $11$ function if and only if every horizontal line intersects that graph at most once Consider the graphs of the functions given in the previous example 1 $f(x)=\sqrt{x}$So the question is that can a 1 to 1 function be equal juice in verse that control the happen Say, if I have ever backs equals one over X and another function say he X equals one over acts They're equal to kill the right and they're also in versus of each other And as you can see, your older the graph of the ABA backs equals one over X


Horizontal Line Test For Function To Have Inverse Expii
Inverse for onetoone functions This area takes functions, but where we usually take values of x and look at the corresponding values of f(x), here we take values of f(x) and look at what value of x produces thisInverse functions with one to one mappingLet's look at an exampleIf we have the function, f x → 3x, and the 'domain' x ∈ {1, 2, 3} Then we see the mappings are for thisThus the graph for inverse function (f1) can be obtained from the graph of the function (f) by switching the position of the y and xaxis How to Calculate Inverse Function (StepWise) Compute the inverse function (f1) of the given function by the following stepsAll of the graphs of these functions satisfy the vertical line test Although the square function and the absolute value function map each value of to exactly one value for , these two functions map two values of to the same value for For example, and lie on both graphs The identity and reciprocal functions, on the other hand, map each to a single value for , and no two map to the
A function can only have an inverse if it is onetoone, ie if we never have f (x 1) = f (x 2) for different elements x 1 and x 2 of the domain This is equivalent to saying that the graph of the function passes the horizontal line test The inverse of f is denoted f1, which should not be confused with the function 1 / f (x)2501 · Horizontal Line Test If every horizontal line, intersects the graph of a function in at most one point, it is a onetoone function Inverse of a Function Defined by Ordered Pairs If \(f(x)\) is a onetoone function whose ordered pairs are of the form \((x,y)\), then its inverse function \(f^{−1}(x)\) is the set of ordered pairs \((y,x)\)If function f is a onetoone function, the graph of the inverse is that of a function If function f is not a one to one, the inverse is a relation but not a function If needed, Free graph paper is available How to Use Inverse Functions Graphing Calculator Enter a formula for function f (2x 1 for example) and press "Plot f(x) and Its
FREE online Tutoring on Thursday nights!Remember, if is a onetoone function, its inverse is a functionThen, to each x in the domain of there is exactly one y in the range (because is a function);and to each y in the range of there is exactly one x in the domain (because is onetoone)The correspondence from the range of back to the domain of is called the inverse function of and is denoted by the symbol Figure 11 illustrates thisIf and only if f(x) = y A function f X → Y is said to be one to one correspondence, if the images of unique elements of X under f are unique, ie, for every x1 , x2 ∈ X, f(x1 ) = f(x2 ) implies x1 = x2 and also range = codomain


Inverse Function


Use The Graph Of A Function To Graph Its Inverse College Algebra
The calculator will find the inverse of the given function, with steps shown If the function is onetoone, there will be a unique inverseIn algebra, we learn that if a function $ f(x) $ has a onetoone mapping, then we can find the inverse function $ f^{1}(x) $ The method that I have seen taught is the "horizontal line test" if any horizontal line touches the graph of the function more than once, then it must not be onetooneSection 28 OnetoOne Functions and Their Inverses What is a Function?


How To Find The Inverse Of A Function 1


Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf
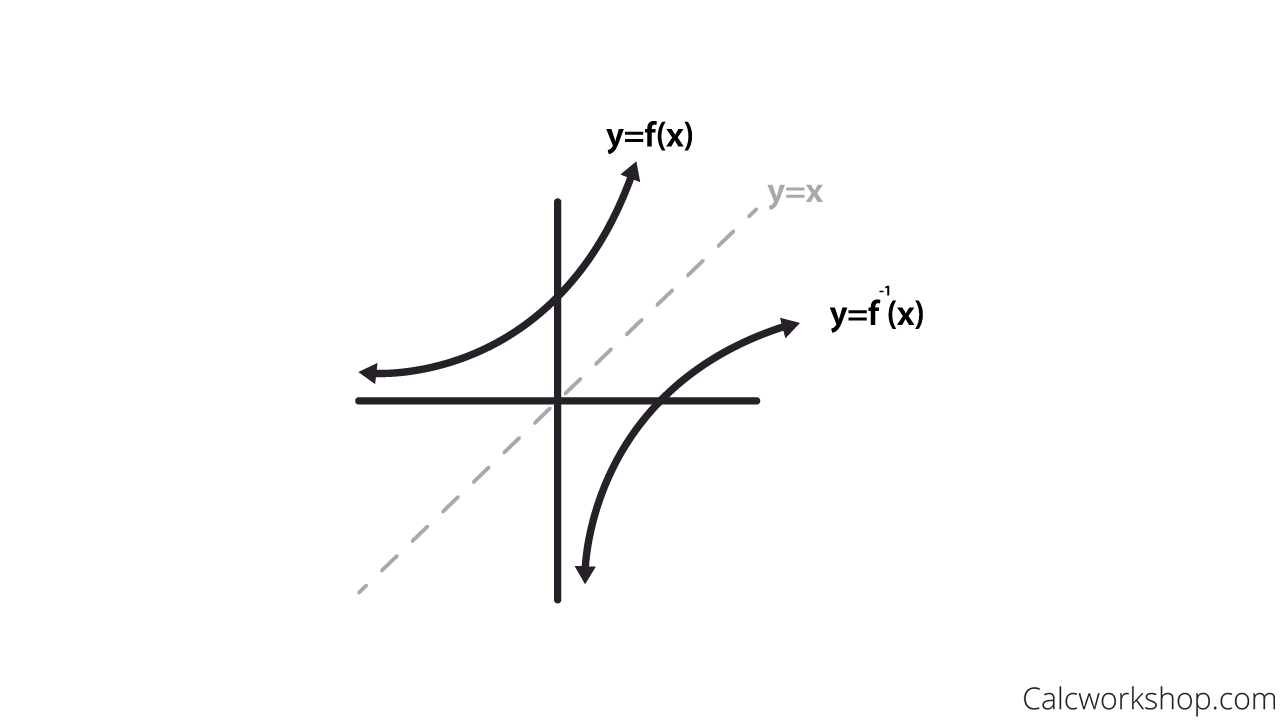
Here it is A function, f (x), has an inverse function if f (x) is onetooneInverse functions rules 4 • Every one to one function has an inverse function, f1(x) • Knowing about inverses helps to work backwards & solve equations • The graph of an inverse function can be found from mirroring the original graph around the line y = x • The domain of the inverse f1(x) is the range of f(x) • The range ofLecture 1 Inverse functions Onetoone Functions A function f is onetoone if it never takes the same value twice or f(x 1) 6=f(x 2) whenever x 1 6=x 2 Example The function f(x) = x is one to one, because if x 1 6=x 2, then f(x 1) 6=f(x 2) On the other hand the function g(x) = x2 is not a onetoone function, because g( 1) = g(1)



Lesson 8


One To One Function One To One Function Graph How To Determine If A Function Is One To One Many To One Function
One to one functions are used in 1) Inverse One to one functions have inverse functions that are also one to one functions 2) Solving certain types of equations Examples 1 To solve equations with logarithms such as ln(2x 3) = ln(4x 2) we deduce the algebraic equation because the ln function is a one to oneGraph the inverse of the onetoone function that is given Our Discord hit 10K members!Inverse Function Summary 1 The inverse function f 1 exists if and only if the function f is one toone 2 The domain of is the same as the range of and the range of is the sa me as the domain of 3 To verify that two one toone functions fg and are inverses of each other , use the composition cancellation equations to show that
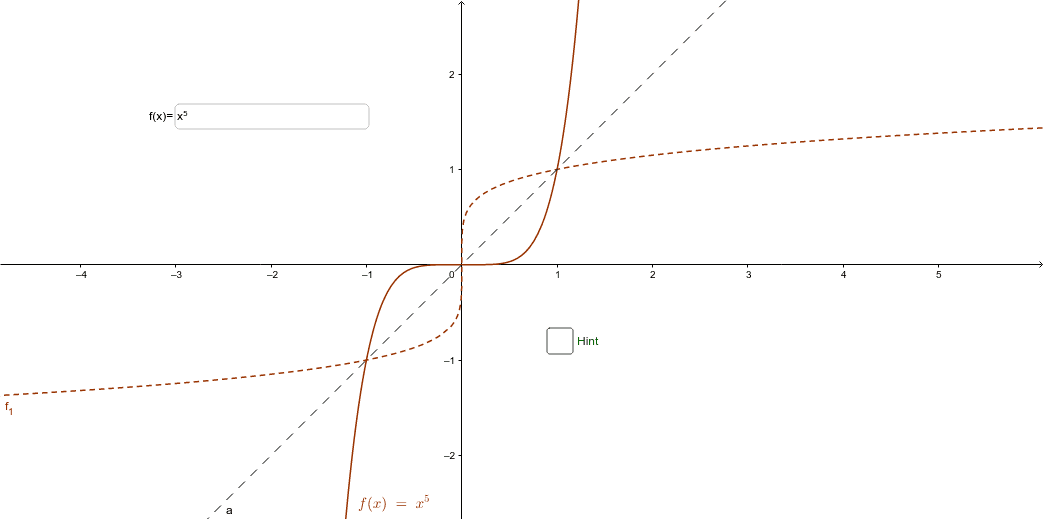


Graph Of An Inverse Function Geogebra


One To One Functions
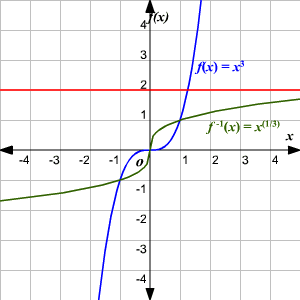
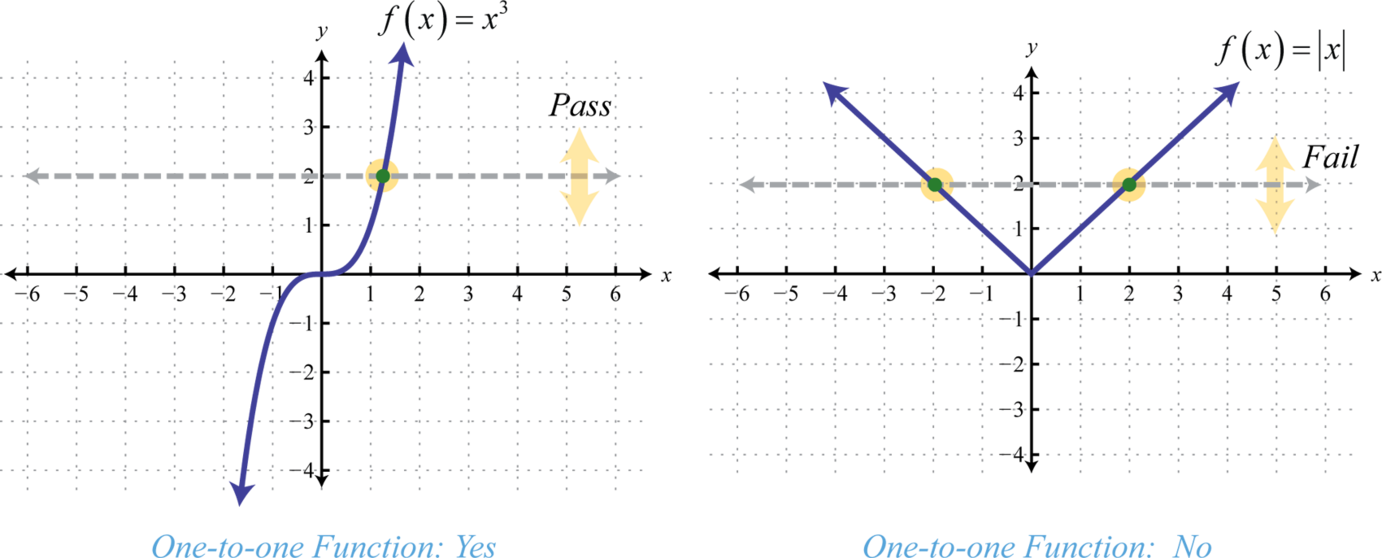
Relationship between inputs (domain) and outputs (range) such that each input produces only one output Passes the vertical line test OK for outputs to be shared OnetoOne Functions A function is a onetoone function if no outputs are shared (each yvalue corresponds to only one xvalue) FormalInverse Functions In this chapter weÕll cover what an inverse functioll is, when a function has an inverse, what inverse functions are useful for, how to graph an inverse function, and how to find the inverse of a function Onetoone Suppose f A Ñ* B is a function We call f onetooneOnetoOne Functions and Their Inverses Consider the function , and its inverse The graphs of these functions are shown below The function f(x) = x 3 is an example of a onetoone function, which is defined as follows A function is onetoone if and only if every element of its range corresponds to at most one element of its domain



Inverse Functions A Simple Guide To Exponential Logarithmic And Inverse Functions



Inverse Functions Solutions Examples Videos
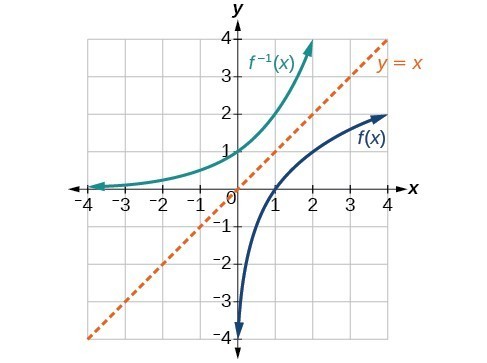
How to find the inverse of onetoone function bellow?If no horizontal line intersects the graph of the function f in more than one point, then the function is 1 to 1 A function f has an inverse f − 1 (read f inverse) if and only if the function is 1 to 1 Properties of a 1 to 1 Function 1) The domain of f equals the range of f –1 and the range of f equals the domain of f − 11706 · The inverse of a function graph is a reflection across the line y = x This is a diagonal line that passes through the origin, with a slope of 1 Graphing inverse functions is accomplished by finding the reflection across the y = x line Take any point on the original function (a,b) and swap each x and y value to find the reflected point, (b, a)


Functions Inverse And Composite Functions


Function Definition Types Examples Facts Britannica
Find a local tutor in you area now!🎉 Meet students and ask top educators your Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6 Problem 7 Problem 8 Problem 9 Problem 10 Problem 11 Problem 12 Problem 13 Problem 14 Problem 15 Problem 16 Problem 17 Problem 18 Problem 19 ProblemHyperbolic Functions Inverses The hyperbolic sine function, \sinh x, is onetoone, and therefore has a welldefined inverse, \sinh^{1} x, shown in blue in the figureIn order to invert the hyperbolic cosine function, however, we need (as with square root) to restrict its domain


Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf
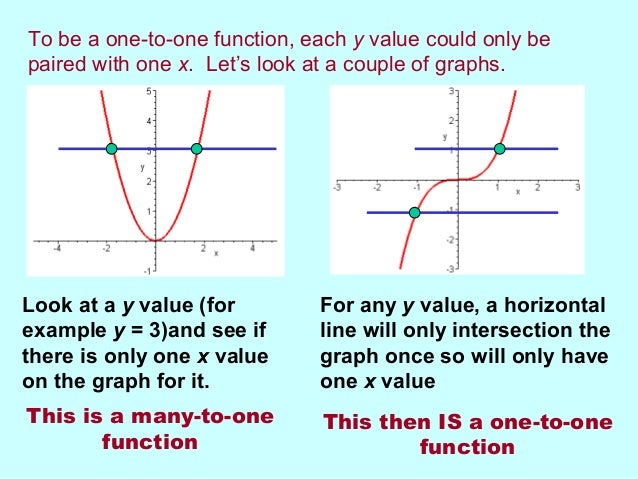


Inverse Functions 2
· In mathematics, an injective function (also known as injection, or onetoone function) is a function that maps distinct elements of its domain to distinct elements of its codomain In other words, every element of the function's codomain is the image of at most one element of its domain The term onetoone function must not be confused with onetoone · The horizontal line test is used for figuring out whether or not the function is an inverse function Picture a upwards parabola that has its vertex at (3,0) Then picture a horizontal line at (0,2) The line will touch the parabola at two points This is how you it's not an inverse function · And determining if a function is OnetoOne is equally simple, as long as we can graph our function But there's even more to an Inverse than just switching our x's and y's As MathBits nicely points out, an Inverse and its Function are reflections of
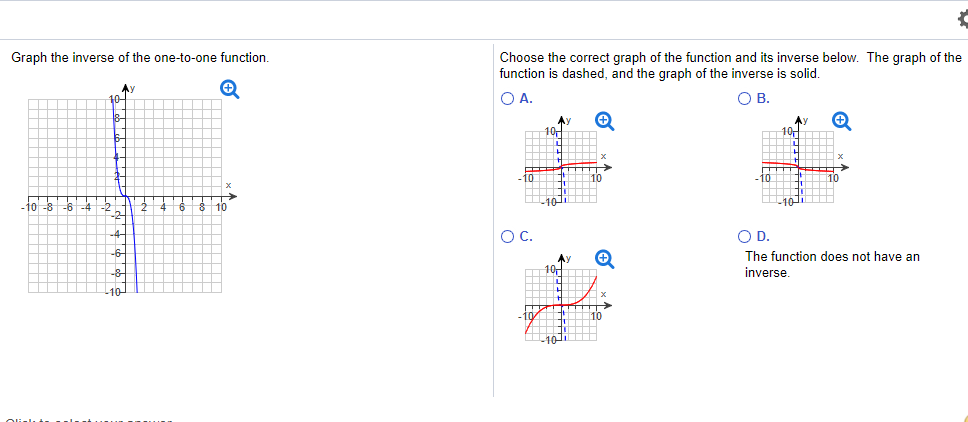


Solved Graph The Inverse Of The One To One Function Choos Chegg Com
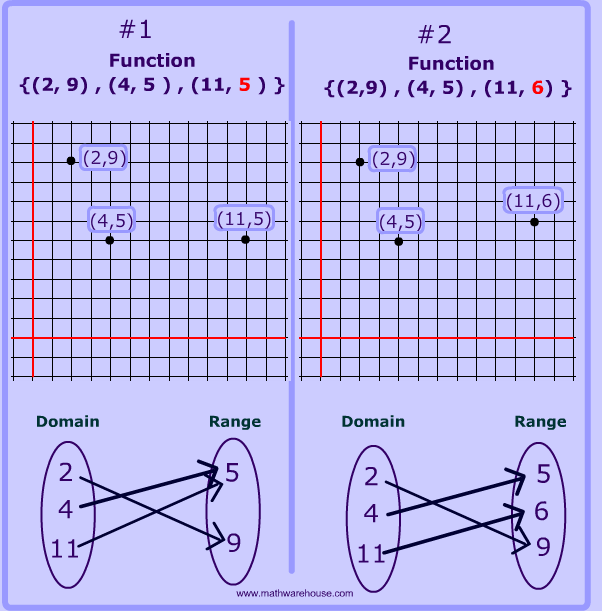


One To One Function Is The Inverse Of A Function A 1 To 1 Function Is Just
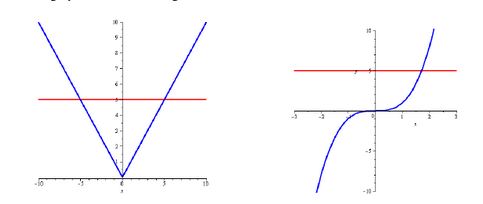
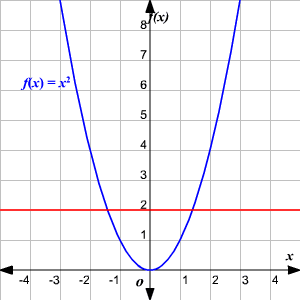
Formally , if "f" is a function which is one to one correspondence, with domain A and range B, then the inverse of function f is given by;Not all functions have an inverse For a function to have an inverse, each element y∈ Ymust correspond to no more than one x∈ X; · If any horizontal line crosses the graph of a function more than once, that means that \(y\)values repeat and the function is not onetoone If no horizontal line crosses the graph of the function more than once, then no \(y\)values repeat and the function is onetoone 3 Yes For example, \(f(x)=\dfrac{1}{x}\) is its own inverse 5
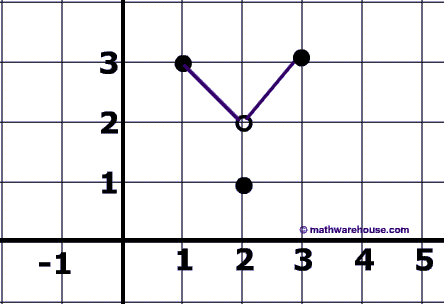


One To One Function Is The Inverse Of A Function A 1 To 1 Function Is Just



Center For Academic Program Support One To One Functions And Inverse Functions
Function Inverse Example 1Practice this lesson yourself on KhanAcademyorg right now https//wwwkhanacademyorg/math/algebra2/functions_and_graphs/functionInverse\f (x)=x^3 inverse\f (x)=\ln (x5) inverse\f (x)=\frac {1} {x^2} inverse\y=\frac {x} {x^26x8} inverse\f (x)=\sqrt {x3} inverse\f (x)=\cos (2x5) inverse\f (x)=\sin (3x) functioninversecalculator enIf we truly have a one to one function then only one value for x matches one value for y, so then y has only one value for x We can denote an inverse of a function with Hold on how do we find the inverse of a set, it's easy all you have to do is switch all the values of x



Lesson Explainer Graphs Of Inverses Of Functions Nagwa



What Is An Inverse Function What Is One To One Waterloo Standard
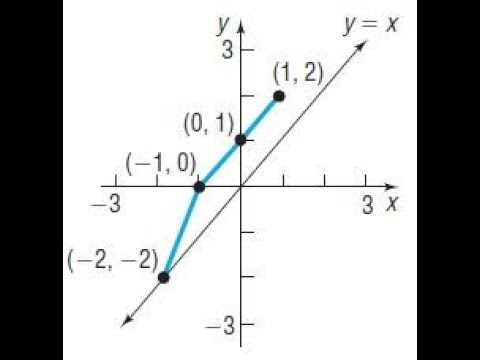
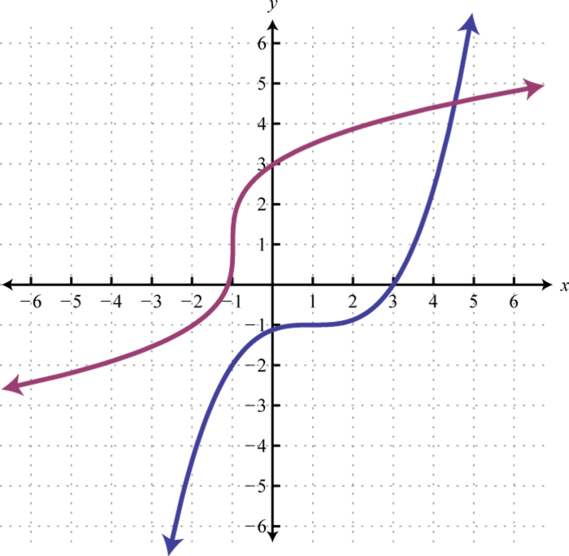
This relationship will be observed for all onetoone functions, because it is a result of the function and its inverse swapping inputs and outputs This is equivalent to interchanging the roles of the vertical and horizontal axes Example 10 Finding the Inverse of a Function Using Reflection about the Identity Line Given the graph of1x Theorem The graph of a function f and the graph of its inverse f 1 are symmetric with respect to the line y = x Symmetry about the line y = x means the x and ycoordinates are switched ex The graph of a onetoone function f is given Draw the graph of f 1 The graph of y = x is also already given a) 4A function fwith this property is called onetoone or an injection If f −1is to be a functionon Y, then each element y∈ Ymust correspond to some x∈ X Functions with this property are called surjections
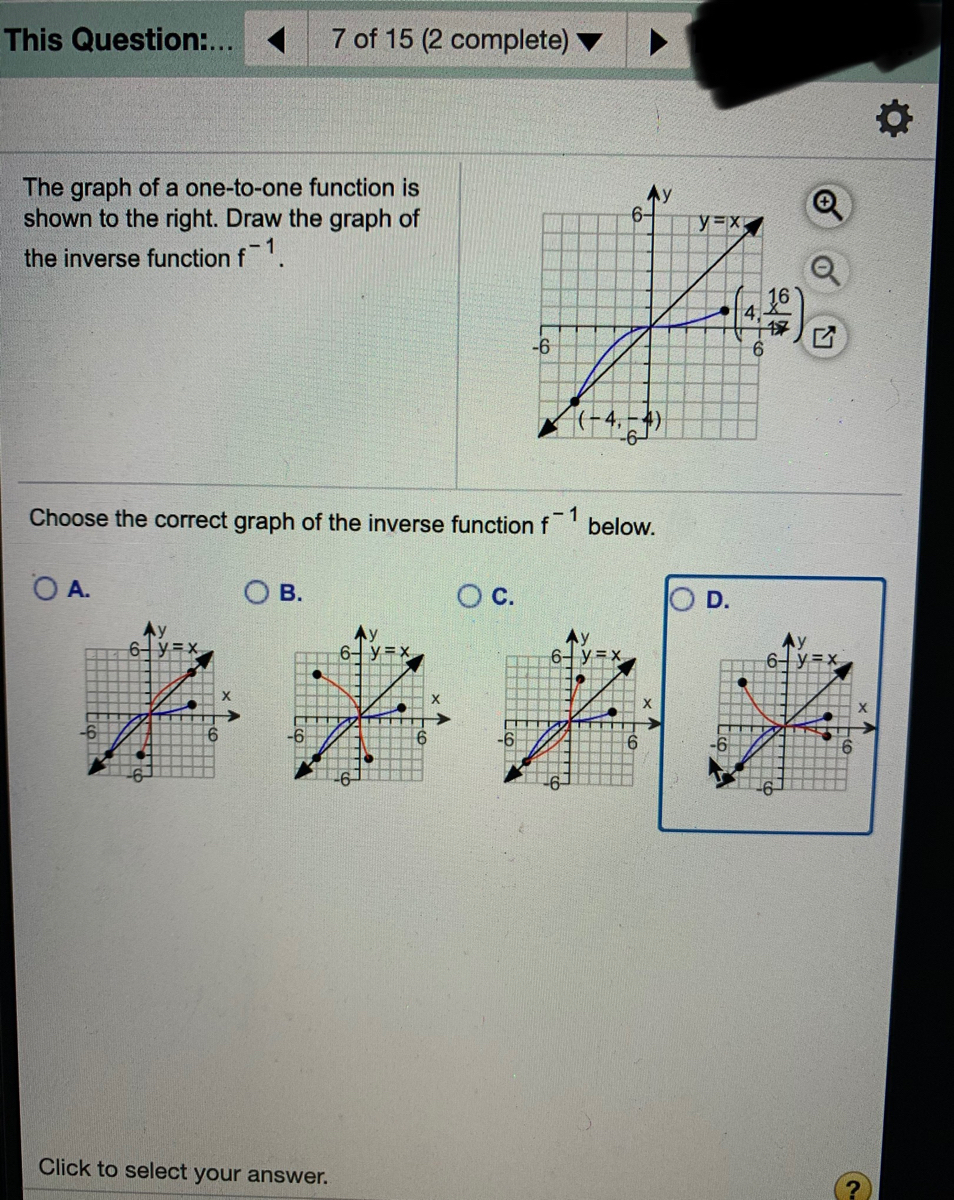


Answered The Graph Of A One To One Function Is Bartleby


Www Humbleisd Net Cms Lib Tx Centricity Domain 35 Section 4 1 exercises Pdf
Get homework help now!141 Determine the conditions for when a function has an inverse 142 Use the horizontal line test to recognize when a function is onetoone 143 Find the inverse of a given function 144 Draw the graph of an inverse function 145 Evaluate inverse trigonometric functionsInverse function Inverse functions are a way to "undo" a function In the original function, plugging in x gives back y, but in the inverse function, plugging in y (as the input) gives back x (as the output) If a function were to contain the point (3,5), its inverse would contain the point (5,3)If the original function is f(x), then its inverse f 1 (x) is not the same as



One To One Functions And Their Inverses Ck 12 Foundation


Use The Graph Of A Function To Graph Its Inverse College Algebra
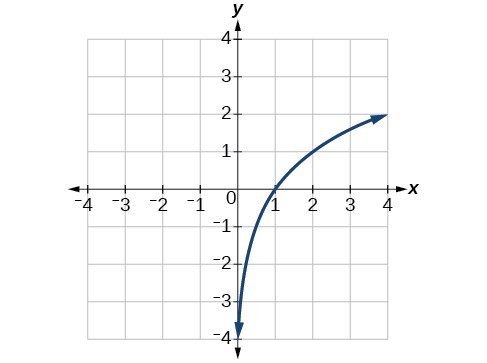
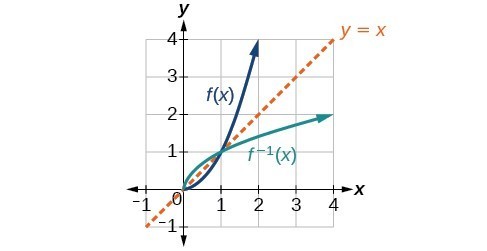
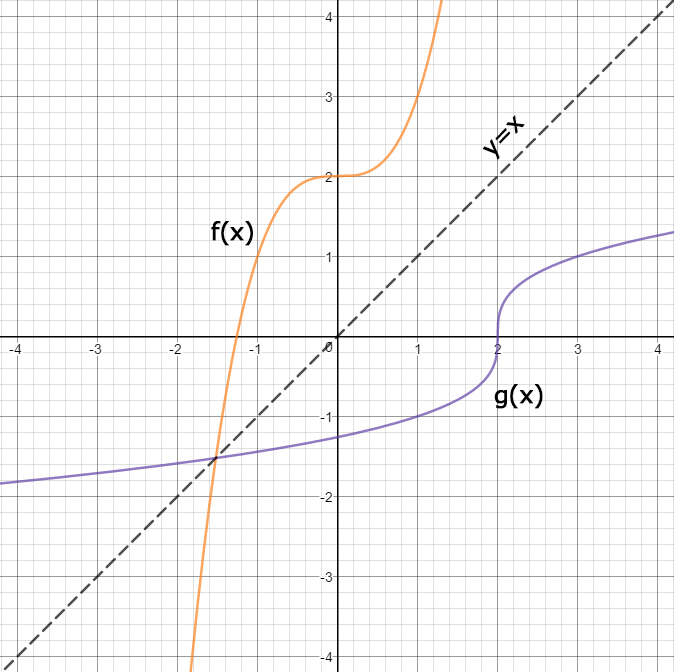
If you're asked to graph the inverse of a function, you can do so by remembering one fact a function and its inverse are reflected over the line y = x This line passes through the origin and has a slope of 1 When you're asked to draw a function and its inverse, you mayA function may have an inverse function even if we cannot find its formula The function \(f (x) = x^5 x 1\) shown in figure (a) is onetoone, so it has an inverse function We can even graph the inverse function, as shown in figure (b), by interchanging the coordinates of points on the graph of \(f\text{}\)The inverse function (Sect 71) I Onetoone functions I The inverse function I The graph of the inverse function I Derivatives of the inverse function The inverse function Remark Only onetoone functions are invertible Definition The inverse of a onetoone function f D → R is the function f −1 R → D defined for all x ∈ D and all y ∈ R as follows


Www Math Utah Edu Wortman 1050 Text If Pdf



Derivatives Of Inverse Functions
F1(y) = x ;All FREE @ http//textbooktacticscom Click show more forThe graph of inverse functions are reflections over the line y = x This means that each xvalue must be matched to one and only one yvalue Functions that


Inverse Of Absolute Value Function Chilimath


Q Tbn And9gct7ztwvpvvordy Mvnjg Qpauy Pioqtn5rwlmoav32m73wqezq Usqp Cau
1210 · Inverse One to One Function Graph The one to one function graph of an inverse one to one function is the reflection of the original graph over the line y = x The original function is y = 2x 1 The new red line is our inverse of y = 2x 1 Note Not all graphs will be a function that produces inverse If the one to one function passes the Horizontal Line Test, its inverse will pass


Solution How To Find The Inverse Of One To One Function Bellow F X 3x 5



The Math Den Graph Of Inverse Functions You Can Also


Q Tbn And9gctmiauoce Jgtrhnhoxjptyptyo5mw4r7aqizegy Baxprcttyz Usqp Cau



In Inverse Functions Why Do We Also Switch The Domain Mathematics Stack Exchange


Inverse Functions Graphs



One To One Functions And Their Inverses Ck 12 Foundation


The Graph Of A One To One Function F Is Given Draw The Inverse F 1 Youtube
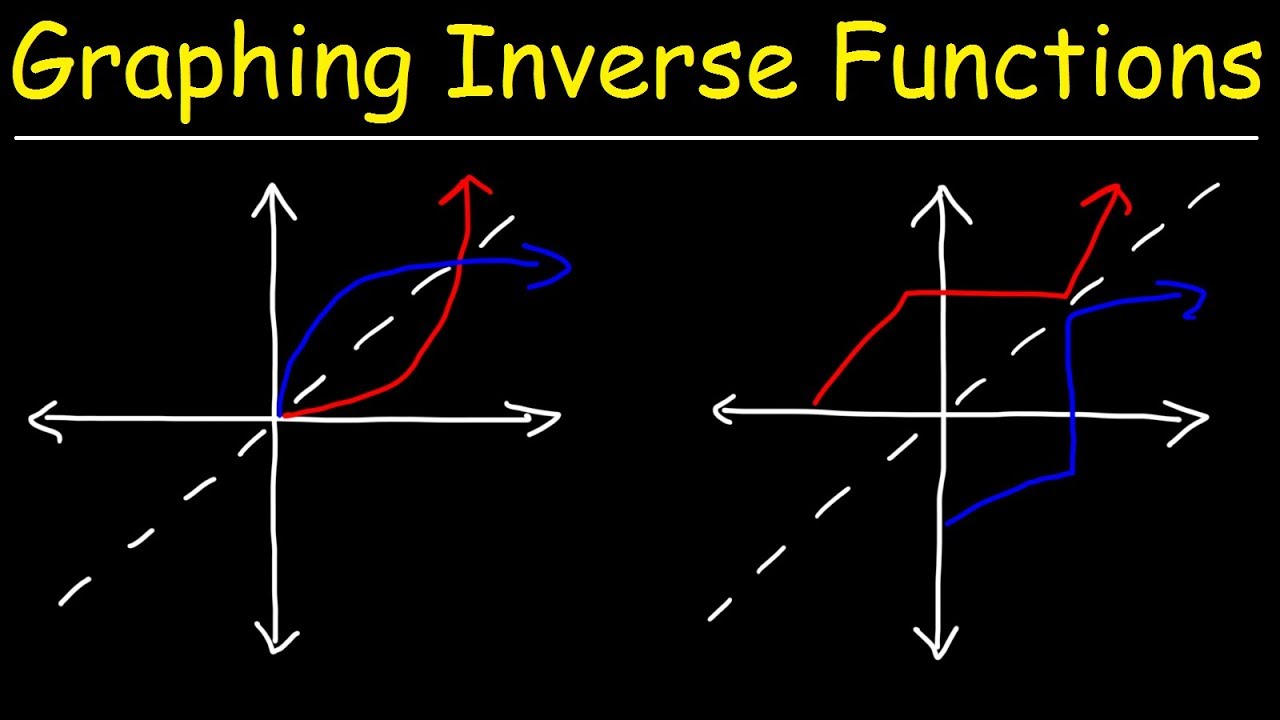


Graphing Inverse Functions Youtube



Solved The Graphs Of One To One Functions Are Given Ske Chegg Com
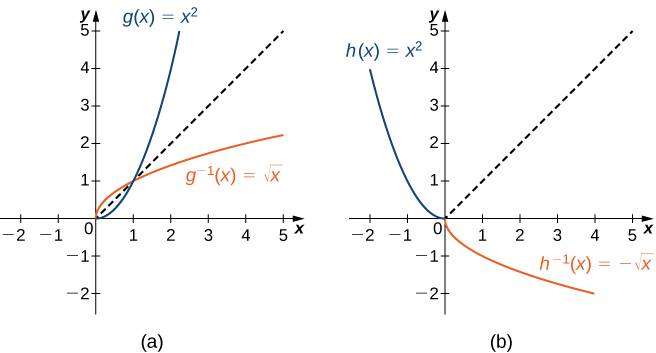


1 4 Inverse Functions Mathematics Libretexts


How To Graph And Find Inverse Functions 19 Terrific Examples
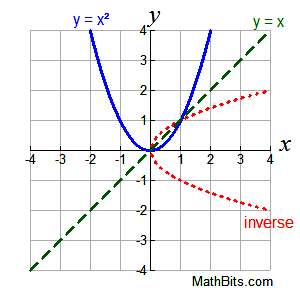


Inverse Of Functions Mathbitsnotebook Ccss Math


Q Tbn And9gcrpavz3g4encmp8sv L9pi Noa6pab0gbavogsjgr3g Tmgnq7z Usqp Cau



One To One Functions Definitions And Examples Video Lesson Transcript Study Com
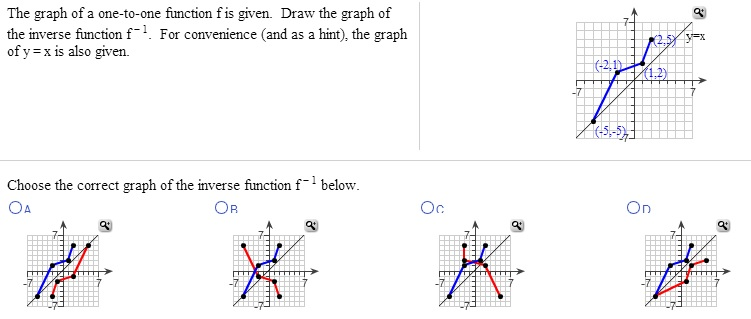


Solved The Graph Of A One To One Function F Is Given Dra Chegg Com



One To One Functions And Their Inverses Ck 12 Foundation


Inverse Functions


Math Psu Edu Sites Default Files Public Migration Section 3 6 class notes new Pdf
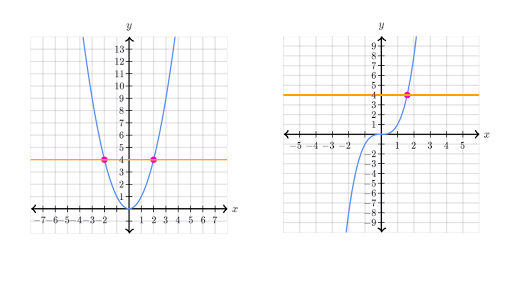


Intro To Invertible Functions Article Khan Academy
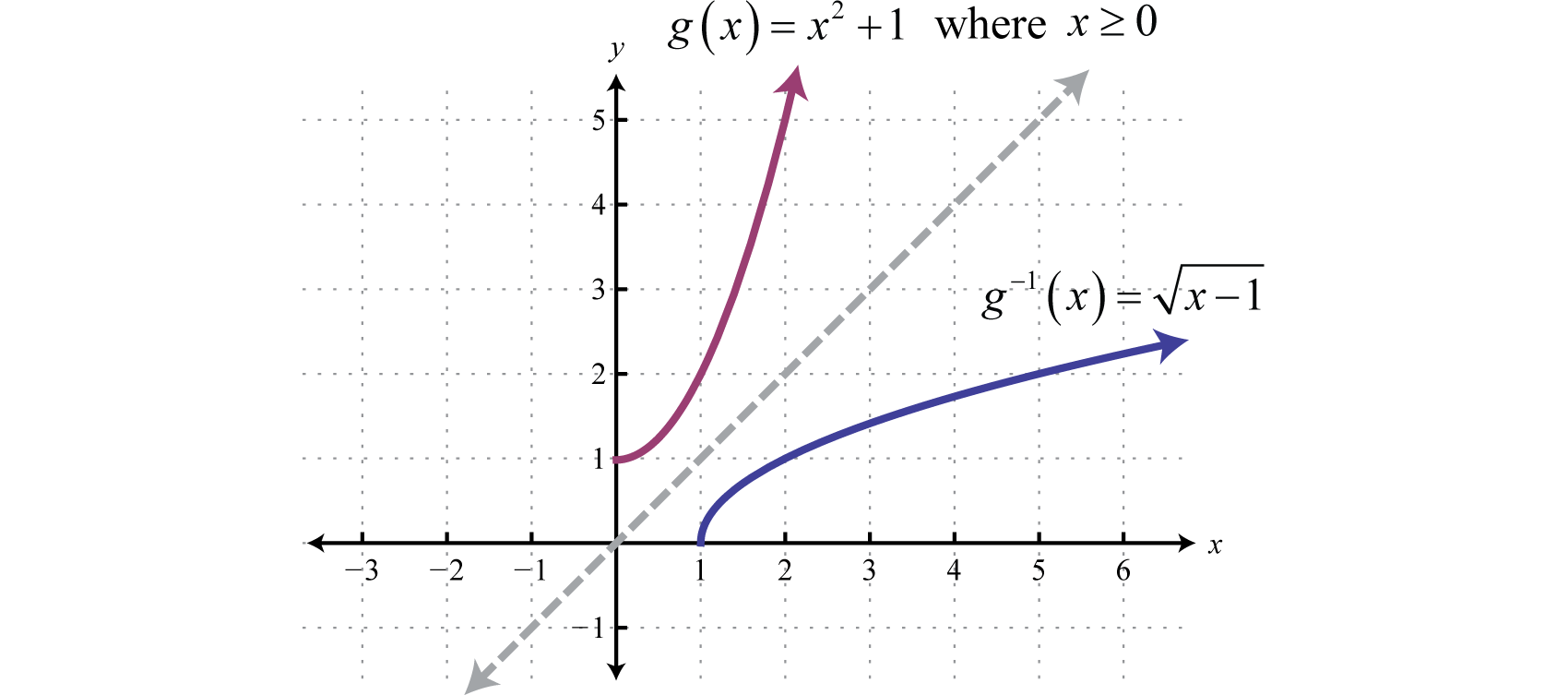


Composition And Inverse Functions


Solved 91 If F It Represents A One To One Function Which Of The Following Could Be The Value Of K 1 3 7 2 11 4 B 92 If G X X2 5 An Course Hero



Horizontal Line Test For Function To Have Inverse Expii
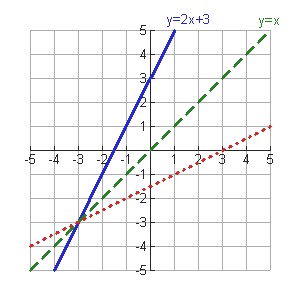


Inverse Of Functions Mathbitsnotebook Ccss Math



5 1 Introduction To Functions


Inverses



Finding The Inverse Of A Function Complete Guide Mashup Math


How To Graph The Inverse Of A Function Dummies



One To One Functions Inverse Functions Mathematics Youtube


How To Tell If A Function Has An Inverse Function One To One 1



Finding Inverse Functions Linear Video Khan Academy



5 1 Introduction To Functions



How To Find The Inverse Of A Function 4 Steps With Pictures



One To One Functions And Their Inverses Ck 12 Foundation
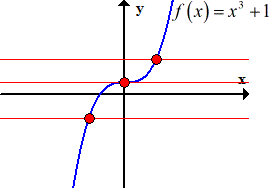


Inverse Of Quadratic Function Chilimath


Inverse Functions


Use The Graph Of A Function To Graph Its Inverse College Algebra



Inverse Function Wikipedia
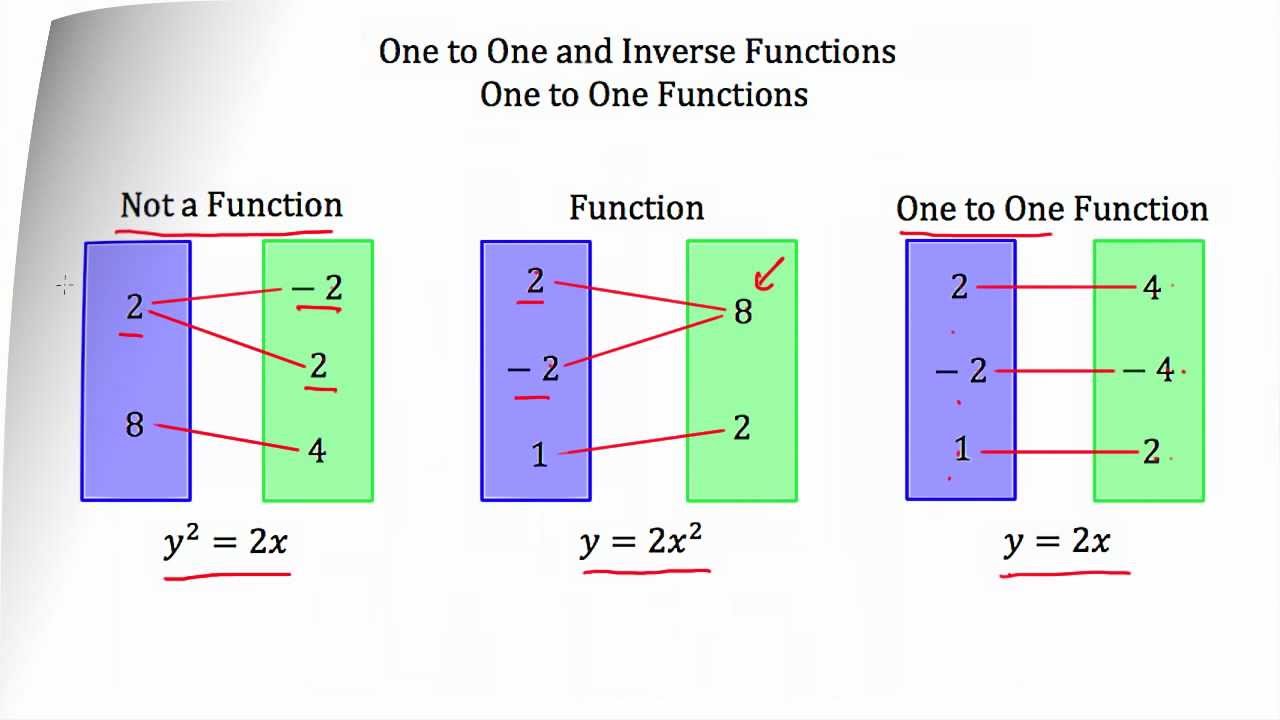


Understanding One To One And Inverse Functions Youtube


One To One Functions


Composition And Inverse Functions


Inverse Functions One To One



Inverse Functions Inverse Operations One To One Functions Inverse Functions Equations Of Inverses An Application Of Inverse Ppt Download


Inverse Functions



Use The Graph Of A Function To Graph Its Inverse College Algebra


Solved The Graph Of A One To One Function F Is Given Draw Chegg Com


Domain Of Inverse Function Expii



Inverse Function Wikipedia


Finding The Inverse Function Graphically Expii



Inverse Functions


Composition And Inverse Functions


Inverse Functions


1



Inverse Functions A Simple Guide To Exponential Logarithmic And Inverse Functions


Algebra Inverse Functions


Solution I Need Help With This Problem Show That The Function F X 1 X 2 Is One To One Via Cketching Its Graph Then Find Its Inverse Function Thank You Very Much


One To One And Onto Functions Nool
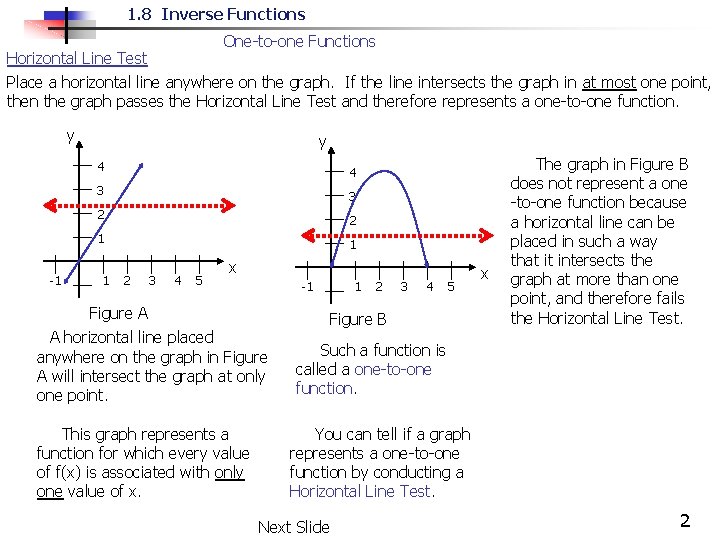


1 8 Inverse Functions Consider The Graphs Of


One To One Functions



One To One Functions And Their Inverses Ck 12 Foundation
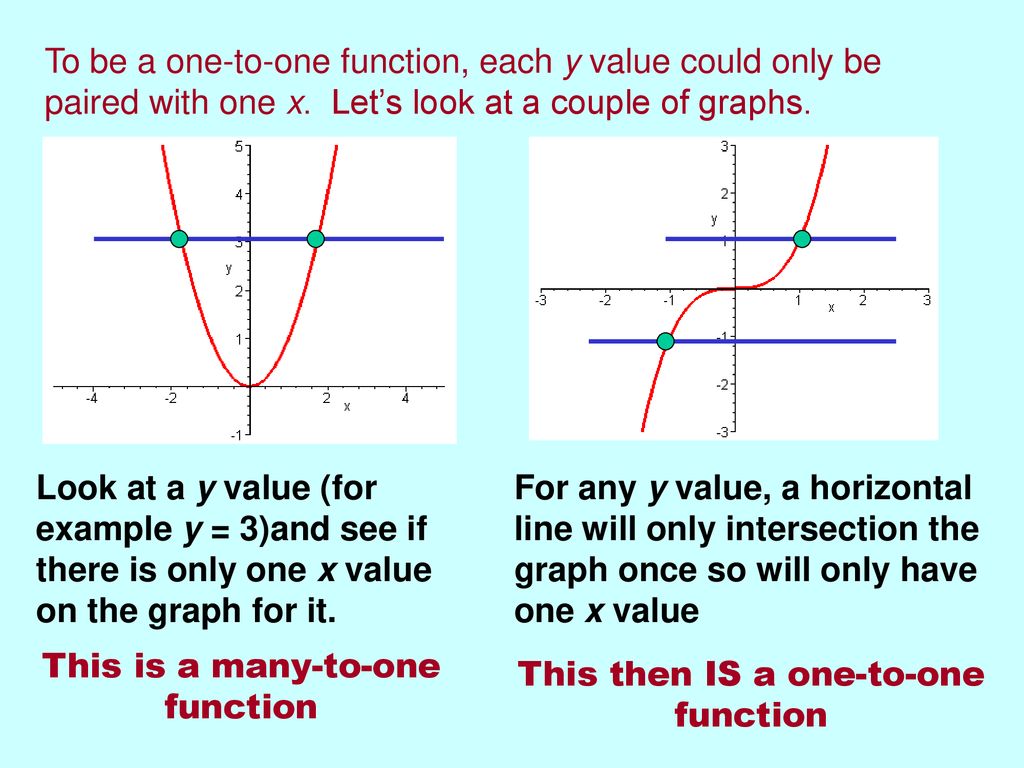


Inverse Functions And Their Graphs Ppt Download



One To One Functions Definitions And Examples Video Lesson Transcript Study Com


How To Find The Derivative Of The Inverse Function At Point When You Have The Original Function The Non Inverse Quora


Inverse Functions



Is A Function S Inverse Also A Function Functions


Links Forward Inverse Trigonometric Functions
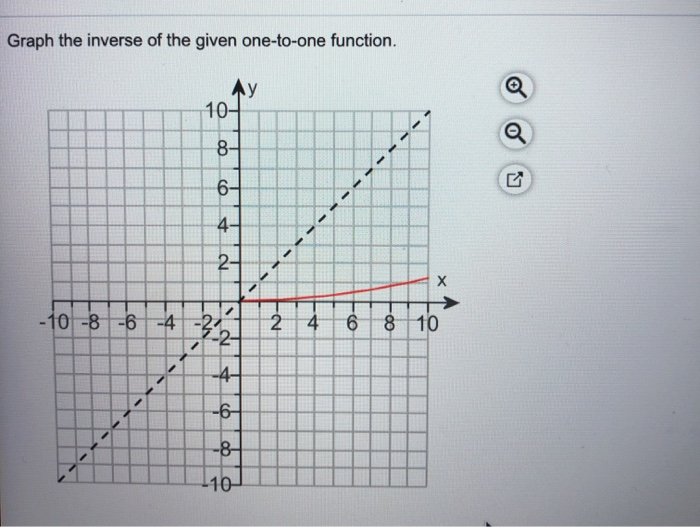


Solved Graph The Inverse Of The Given One To One Function Chegg Com
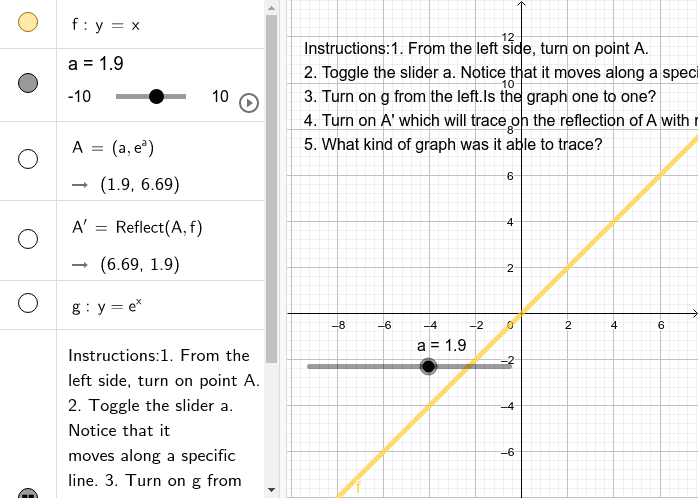


Inverse Function Conjectures Geogebra
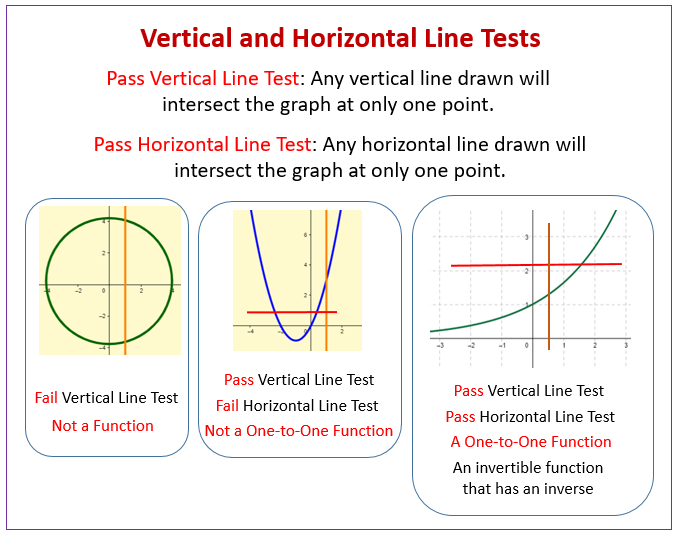


Inverse Functions Examples Solutions Videos Activities


How To Graph And Find Inverse Functions 19 Terrific Examples


Answered The Graph Of A One To One Function F Is Bartleby


Inverse Functions One To One


Composition And Inverse Functions
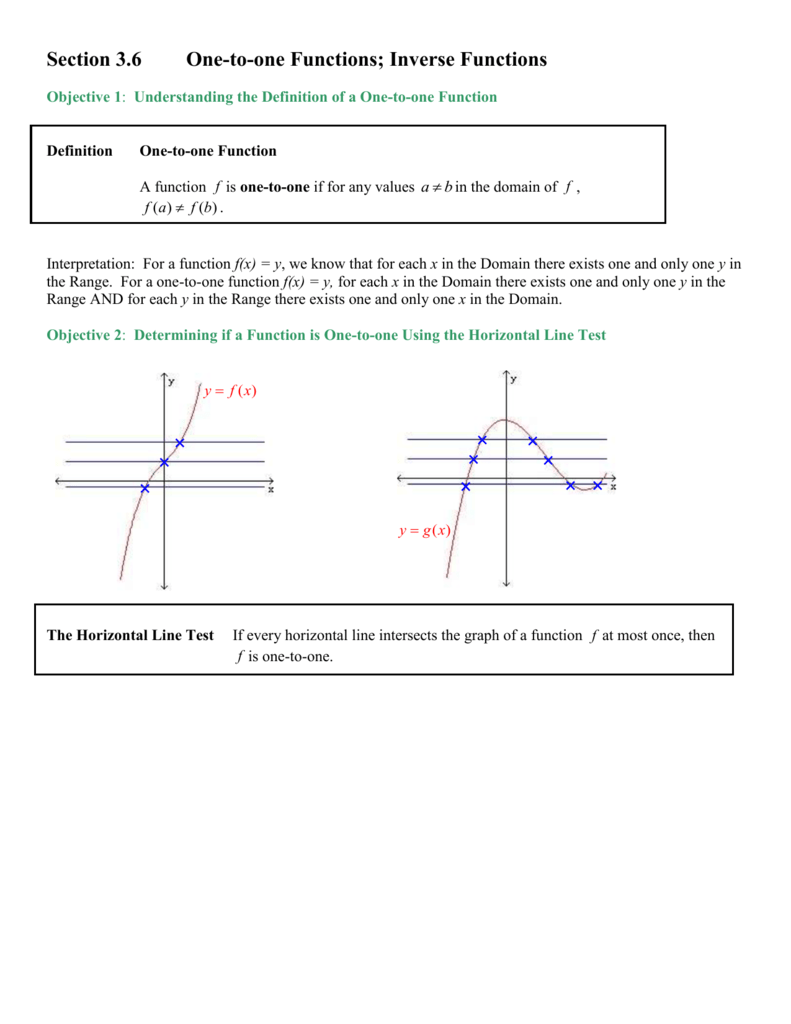


Sec 3 6
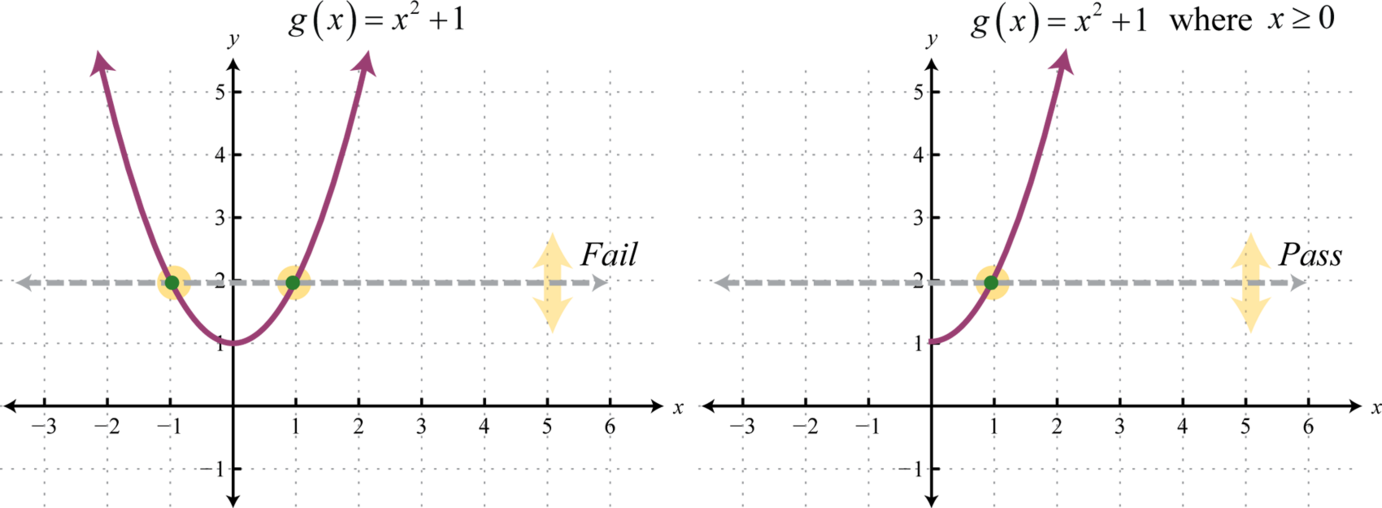


Composition And Inverse Functions


Biomath Functions



1 4 Inverse Functions Mathematics Libretexts



0 件のコメント:
コメントを投稿